3D Gaussian Splatting 1
Published:
Here is my attempt to understand the rasterisation part in 3D Gaussian splatting pipeline. While undertaking my master’s thesis in 3DGS at University College London, I had to understand each part of the pipeline in depth and was fascinated with the forward pass rasterisation part which was responsible to create an image from many (thousands or even millions!!) of 3D Gaussian Primitive.
(1/3) Understanding Spherical Harmonics coefficients
Aim : For every 3D gaussian primitive, describe a function for RGB colour values that are view direction dependent
For reference here
\[\newcommand{\Ksqrt}[2]{\sqrt{\frac{(2\cdot #1+1)}{4\pi} \cdot \frac{(#1-|#2|)!}{(#1+|#2|)!}}}\]Basis functions
Any function can be represented as a linear combination of basis functions. In our case we interested in describing a function for RGB colour values which is view direction dependent. For our case we will be focussing on Associated Legendre polynomials which will act as basis functions.
Associated Legendre polynomials
The associated Legendre polynomials \(P_l^m(x)\) and \(P_l^{-m}(x)\) generalise the Legendre polynomials \(P_l(x)\) and are solutions to the associated Legendre differential equation, where degree \(l\) is a positive integer and order \(m=0, 1 \ldots l\).
Same degree polynomials are orthogonal w.r.t. a constant term and between different degrees they are orthogonal with a different constant.
The first few associated Legendre polynomials are given by the following expressions given here. I will list down the relevant ones for the purpose of this post wrt to \(\cos\theta\) as argument.
Degree \(l= 0\), Order \(m= 0\)
\[\begin{align} P^0_0(\cos\theta)= 1 \end{align}\]Degree \(l= 1\), Order \(m= 0,1\)
\[\begin{align} P^{0}_1(\cos\theta) &= \cos\theta \\ P^{1}_1(\cos\theta) &= -\sqrt{1- \cos^2\theta} \\ &= -\sin\theta \end{align}\]Degree \(l= 2\), Order \(m= 0,1,2\)
\[\begin{align} P_{2}^{0}(\cos\theta) &= \frac{1}{2} \left(3 \cos^2\theta - 1\right) \\ P_{2}^{1}(\cos\theta) &= -3\cos\theta \sqrt{1- \cos^2\theta} \\ &= -3\cos\theta \sin\theta \\ P_{2}^{2}(\cos\theta) &= 3 (1- \cos^2\theta) \\ &= 3 \sin^2\theta \end{align}\]Degree \(l= 3\), Order \(m= 0,1,2,3\)
\[\begin{align} P_{3}^{0}(\cos\theta) &= \frac{1}{2} \cos\theta\left(5 \cos^\theta - 3 \right) \\ P_{3}^{1}(\cos\theta) &= \frac{3}{2} (1- 5\cos^2\theta) \sqrt{1- \cos^2\theta} \\ &= \frac{3}{2} (1- 5\cos^2\theta) \sin\theta \\ P_{3}^{2}(\cos\theta) &= 15 \cos\theta (1- \cos\theta) \\ &= 15 \cos\theta \sin^2\theta \\ P_{3}^{3}(\cos\theta) &= -15 \left( 1- \cos^2\theta \right)^{\frac{3}{2}} \\ &= -15 \sin^3\theta \end{align}\]Spherical Harmonics coefficients
Spherical harmonics are the solution of Laplace’s equation in spherical coordinates.
The conversion from cartesian to spherical coordinates (Figure 1) for a unit vector is simply
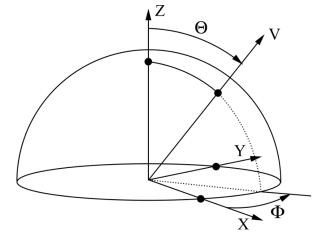
Where \(K_{l}^{m}\) is the normalising constant defined as \(K_{l}^{m}= \Ksqrt{l}{m}\) Since we are taking the absolute value of \(m\) in the above equation, \(K_{l}^{m} = K_{l}^{-m}\)
And now we calculate the coefficients for each degree and order of the spherical harmonics. The exact values of these codes is used in the code can be seen here
Degree \(l = 0\)
\(m=0\)
\[\begin{align} Y_{l=0}^{m=0}(\theta, \phi) &= K_{0}^{0} \cdot P_{0}^{0}(\cos\theta) \\ &= \Ksqrt{0}{0} \cdot 1 \\ &= \frac{1}{2}\sqrt{\frac{1}{\pi}} \\ &= 0.28209479177387814 \end{align}\]Degree 0 spherical harmonics coefficient is defined and used can be seen here:
C0 = 0.28209479177387814
# (Other intermediate lines of code are omitted for brevity)
result = C0 * sh[..., 0]
Degree \(l= 1\)
\(m=-1\)
\[\begin{align} Y_{l=1}^{m=-1}(\theta, \phi) &= \sqrt{2} \cdot K_{1}^{-1} \cdot \sin(-(-1)\phi) \cdot P_{1}^{-(-1)}(\cos\theta) \\ &= \sqrt{2} \cdot \Ksqrt{1}{-1} \cdot \sin(\phi) \cdot -\sqrt{(1-\cos^2\theta)} \\ &= -\frac{1}{2} \sqrt{\frac{3}{\pi}} \cdot \sin(\phi) \cdot \sin(\theta) \\ &= -0.4886025119029199 \cdot \sin(\phi) \cdot \sin(\theta) \\ &= -0.4886025119029199 \cdot y \end{align}\]\(m=0\)
\[\begin{align} Y_{l=1}^{m=0}(\theta, \phi) &= K_{1}^{0} \cdot \cos(0\cdot\phi) \cdot P_{1}^{0}(\cos\theta) \\ &= \Ksqrt{1}{0} \cdot \cos\theta \\ &= \frac{1}{2} \cdot \sqrt{\frac{3}{\pi}} \cdot \cos(\theta )\\ &= 0.4886025119029199 \cdot \cos(\theta ) \\ &= 0.4886025119029199 \cdot z \end{align}\]\(m=1\)
\[\begin{align} Y_{l=1}^{m=1}(\theta, \phi) &= \sqrt{2} \cdot K_{1}^{1} \cdot \cos(1\cdot\phi) \cdot P_{1}^{1}(\cos\theta) \\ &= \sqrt{2} \cdot \Ksqrt{1}{1} \cdot \cos(\phi) \cdot -\sqrt{(1-\cos^2\theta)} \\ &= -\frac{1}{2} \sqrt{\frac{3}{\pi}} \cdot \cos(\phi) \cdot \sin(\theta) \\ &= -0.4886025119029199 \cdot \cos(\phi) \cdot \sin(\theta) \\ &= -0.4886025119029199 \cdot x \end{align}\]In the code, the coefficients are defined as:
C1 = 0.4886025119029199
C2 = [
1.0925484305920792,
-1.0925484305920792,
0.31539156525252005,
-1.0925484305920792,
0.5462742152960396
]
C3 = [
-0.5900435899266435,
2.890611442640554,
-0.4570457994644658,
0.3731763325901154,
-0.4570457994644658,
1.445305721320277,
-0.5900435899266435
]
# (Other intermediate lines of code are omitted for brevity)
x, y, z = dirs[..., 0:1], dirs[..., 1:2], dirs[..., 2:3]
result = (result -
C1 * y * sh[..., 1] +
C1 * z * sh[..., 2] -
C1 * x * sh[..., 3])
Degree \(l= 2\)
\(m=-2\)
\[\begin{align} Y_{l=2}^{m=-2}(\theta, \phi) &= \sqrt{2} \cdot K_{2}^{-2} \cdot \sin(-(-2)\phi) \cdot P_{2}^{-(-2)}(\cos\theta) \\ &= \sqrt{2} \cdot \Ksqrt{2}{-2} \cdot \sin(2\phi) \cdot 3 \cdot (1- \cos^2\theta) \\ &= \frac{1}{4} \sqrt{\frac{15}{\pi}}\cdot 2 \sin\phi \cos\phi \cdot \sin^2\theta \\ &= \frac{1}{2} \sqrt{\frac{15}{\pi}} \cdot (\sin\phi \sin\theta) \cdot (\cos \phi \sin\theta) \\ &= 1.0925484305920792 \cdot (\sin\phi \sin\theta) \cdot (\cos \phi \sin\theta)\\ &= 1.0925484305920792 \cdot x \cdot y \end{align}\]\(m=-1\)
\(\begin{align} Y_{l=2}^{m=-1}(\theta, \phi) &= \sqrt{2} \cdot K_{2}^{-1} \cdot \sin(-(-1)\phi) \cdot P_{2}^{-(-1)}(\cos\theta) \\ &= \sqrt{2} \cdot \Ksqrt{2}{-1} \sin\phi \cdot (-3) \cos\theta \sin\theta \\ &= -\frac{1}{2} \sqrt{\frac{15}{\pi}} (\sin\phi \sin\theta )(\cos\theta) \\ &= -1.0925484305920792 \cdot (\sin\phi \sin\theta )(\cos\theta)\\ &= -1.0925484305920792 \cdot y \cdot z \end{align}\)
\(m=0\)
\(\begin{align} Y_{l=2}^{m=0}(\theta, \phi) &= K_{2}^{0} \cdot P_{2}^{0}(\cos\theta) \\ &= \Ksqrt{2}{0} \cdot \left(\frac{1}{2}(3\cos^2\theta - 1)\right) \\ &= \frac{1}{4} \sqrt{\frac{5}{\pi}} \cdot (3\cos^2\theta - 1) \\ &= \frac{1}{4} \sqrt{\frac{5}{\pi}} \cdot (2\cos^2\theta + [\cos^2\theta-1]\cdot 1) \\ &= \frac{1}{4} \sqrt{\frac{5}{\pi}} \cdot (2\cos^2\theta + [-\sin^2\theta]\cdot [\cos^2 \phi+ \sin^2 \phi]) \\ &= \frac{1}{4} \sqrt{\frac{5}{\pi}} \cdot (2\cos^2\theta + [-(\sin\theta \cos \phi)^2+ (\sin\theta \sin\phi)^2]) \\ &= 0.31539156525252005 \cdot [2 z^2- x^2 - y^2] \end{align}\)
\(m=1\)
\(\begin{align} Y_{l=2}^{m=1}(\theta, \phi) &= \sqrt{2} \cdot K_{2}^{1} \cdot \cos\phi \cdot P_{2}^{1}(\cos\theta) \\ &= \sqrt{2} \cdot \Ksqrt{2}{1} \cdot \cos\phi \cdot (-3 \cos\theta \sin\theta) \\ &= -\frac{1}{2} \sqrt{\frac{15}{\pi}} \cdot (\cos\phi \sin\theta) (\cos\theta ) \\ &= -1.0925484305920792 \cdot (\cos\phi \sin\theta) (\cos\theta )\\ &= -1.0925484305920792 \cdot x \cdot z \end{align}\)
\(m=2\)
\(\begin{align} Y_{l=2}^{m=2}(\theta, \phi) &= \sqrt{2} \cdot K_{2}^{2} \cdot \cos(2\phi) \cdot P_{2}^{2}(\cos\theta) \\ &= \sqrt{2} \cdot \Ksqrt{2}{2} \cdot \cos(2\phi) \cdot 3 \sin^2\theta \\ &= \frac{1}{4} \sqrt{\frac{15}{\pi}} \cdot [\cos(2\phi) \cdot \sin^2\theta] \\ &= \frac{1}{4} \sqrt{\frac{15}{\pi}} \cdot [\cos^2\phi - \sin^2\phi] \cdot \sin^2\theta \\ &= \frac{1}{4} \sqrt{\frac{15}{\pi}} \cdot [(\cos\phi \sin\theta)^2 - (\sin\phi \sin\theta)^2] \\ &= 0.5462742152960396 \cdot [x^2 - y^2] \end{align}\)
In the code the coefficients are defined as:
C2 = [
1.0925484305920792,
-1.0925484305920792,
0.31539156525252005,
-1.0925484305920792,
0.5462742152960396
]
# (Other intermediate lines of code are omitted for brevity)
xx, yy, zz = x * x, y * y, z * z
xy, yz, xz = x * y, y * z, x * z
result = (result +
C2[0] * xy * sh[..., 4] +
C2[1] * yz * sh[..., 5] +
C2[2] * (2.0 * zz - xx - yy) * sh[..., 6] +
C2[3] * xz * sh[..., 7] +
C2[4] * (xx - yy) * sh[..., 8])
Degree \(l= 3\)
\(m=-3\)
\[\begin{align} Y_{l=3}^{m=-3}(\theta, \phi) &= \sqrt{2} \cdot K_{3}^{-3} \cdot \sin(-(-3)\phi) \cdot P_{3}^{-(-3)}(\cos\theta) \\ &= \sqrt{2} \cdot \Ksqrt{3}{3} \cdot \sin(3\phi) \cdot (-15 \sin^3\theta) \\ &= -\frac{1}{4} \sqrt{\frac{35}{2\pi}} \cdot (\sin(3\phi) \cdot \sin^3\theta \\ &= -\frac{1}{4} \sqrt{\frac{35}{2\pi}} \cdot (3 \sin\phi- 4\sin^3\phi) \cdot \sin^3\theta \\ &= -\frac{1}{4} \sqrt{\frac{35}{2\pi}} \cdot (\sin\theta \sin\phi) [\sin^2\theta (3- 3 \sin^2\phi- \sin^2\phi) ] \\ &= -\frac{1}{4} \sqrt{\frac{35}{2\pi}} \cdot (\sin\theta \sin\phi) [\sin^2\theta (3\cos^2\phi- \sin^2\phi) ] \\ &= -\frac{1}{4} \sqrt{\frac{35}{2\pi}} \cdot [\sin\theta \sin\phi) [3 \sin^2\theta \cos^2\phi- \sin^2\theta \sin^2\phi) \\ &= -0.5900435899266435 \cdot y \cdot (3x^2 - y^2) \end{align}\]\(m=-2\)
\[\begin{align} Y_{l=3}^{m=-2}(\theta, \phi) &= \sqrt{2} \cdot K_{3}^{-2} \cdot \sin(-(-2)\phi) \cdot P_{3}^{-(-2)}(\cos\theta) \\ &= \sqrt{2} \cdot \Ksqrt{3}{2} \cdot \sin(2\phi) \cdot (15 \cos\theta \sin^2\theta) \\ &= \frac{1}{2} \sqrt{\frac{105}{\pi}} \cdot (\sin\phi \cos\phi) \cdot (\cos\theta \sin^2\theta) \\ &= \frac{1}{2} \sqrt{\frac{105}{\pi}} \cdot (\cos\theta) (\sin\theta \sin\phi) (\sin\theta \cos\phi) \\ &= 2.890611442640554 \cdot z \cdot y \cdot x \end{align}\]\(m=-1\)
\[\begin{align} Y_{l=3}^{m=-1}(\theta, \phi) &= \sqrt{2} \cdot K_{3}^{-1} \cdot \sin(-(-1)\phi) \cdot P_{3}^{-(-1)}(\cos\theta) \\ &= \sqrt{2} \cdot \Ksqrt{3}{1} \cdot \sin(\phi) \cdot \frac{3}{2} (1- 5 \cos^2\theta ) \sin\theta \\ &= \frac{1}{4} \sqrt{\frac{21}{2\pi}} \cdot (\sin\phi \sin\theta) \cdot \left(1- 5 \cos^2\theta \right) \\ &= -\frac{1}{4} \sqrt{\frac{21}{2\pi}} \cdot (\sin\phi \sin\theta) \cdot \left[4 \cos^2\theta+ (\cos^2\theta - 1)\cdot 1 \right] \\ &= -\frac{1}{4} \sqrt{\frac{21}{2\pi}} \cdot (\sin\phi \sin\theta) \cdot \left[4 \cos^2\theta+ (-\sin^2\theta)\cdot(\sin^2\phi + \cos^2\phi) \right] \\ &= -\frac{1}{4} \sqrt{\frac{21}{2\pi}} \cdot (\sin\phi \sin\theta) \cdot \left[4 \cos^2\theta+ (-\sin^2\theta)\cdot(\sin^2\phi + \cos^2\phi) \right] \\ &= -\frac{1}{4} \sqrt{\frac{21}{2\pi}} \cdot (\sin\phi \sin\theta) \cdot \left(4 \cos^2\theta - \sin^2\theta\sin^2\phi -\sin^2\theta \cos^2\phi \right) \\ &= 0.4570457994644658 \cdot y \cdot (4z^2 - x^2 - y^2) \end{align}\]\(m=0\)
\[\begin{align} Y_{l=3}^{m=0}(\theta, \phi) &= K_{3}^{0} \cdot P_{3}^{0}(\cos\theta) \\ &= \Ksqrt{3}{0} \cdot \frac{1}{2} \left(5 \cos^3\theta - 3 \cos\theta\right) \\ &= \frac{1}{4} \sqrt{\frac{7}{\pi}} \cdot \left(5 \cos^3\theta - 3 \cos\theta\right) \\ &= \frac{1}{4} \sqrt{\frac{7}{\pi}} \cdot \cos\theta \cdot \left(5 \cos^2\theta - 3 \right) \\ &= \frac{1}{4} \sqrt{\frac{7}{\pi}} \cdot \cos\theta \cdot \left[2 \cos^2\theta +(3\cos^2\theta- 3)\cdot 1 \right] \\ &= \frac{1}{4} \sqrt{\frac{7}{\pi}} \cdot \cos\theta \cdot \left[2 \cos^2\theta +(-3\sin^2\theta)\cdot (\sin^2\phi+ \cos^2\phi) \right] \\ &= \frac{1}{4} \sqrt{\frac{7}{\pi}} \cdot \cos\theta \cdot \left(2 \cos^2\theta -3\sin^2\theta\sin^2\phi -3\sin^2\theta\cos^2\phi \right) \\ &= 0.3731763325901154 \cdot z \cdot (2z^2 - 3x^2 - 3y^2) \end{align}\]\(m=1\)
\[\begin{align} Y_{l=3}^{m=1}(\theta, \phi) &= \sqrt{2} \cdot K_{3}^{1} \cdot \cos\phi \cdot P_{3}^{1}(\cos\theta) \\ &= \sqrt{2} \cdot \Ksqrt{3}{1} \cdot \cos\phi \cdot \frac{3}{2} (5 \cos^2\theta - 1) \sin\theta \\ &= \frac{1}{4} \sqrt{\frac{21}{2\pi}} \cdot (\cos\phi \sin\theta) \cdot (5 \cos^2\theta - 1) \\ &= -\frac{1}{4} \sqrt{\frac{21}{2\pi}} \cdot (\cos\phi \sin\theta) \cdot \left(1- 5 \cos^2\theta \right) \\ &= -\frac{1}{4} \sqrt{\frac{21}{2\pi}} \cdot (\cos\phi \sin\theta) \cdot \left[4 \cos^2\theta+ (\cos^2\theta - 1)\cdot 1 \right] \\ &= -\frac{1}{4} \sqrt{\frac{21}{2\pi}} \cdot (\cos\phi \sin\theta) \cdot \left[4 \cos^2\theta+ (-\sin^2\theta)\cdot(\sin^2\phi + \cos^2\phi) \right] \\ &= -\frac{1}{4} \sqrt{\frac{21}{2\pi}} \cdot (\cos\phi \sin\theta) \cdot \left[4 \cos^2\theta+ (-\sin^2\theta)\cdot(\sin^2\phi + \cos^2\phi) \right] \\ &= -\frac{1}{4} \sqrt{\frac{21}{2\pi}} \cdot (\cos\phi \sin\theta) \cdot \left(4 \cos^2\theta - \sin^2\theta\sin^2\phi -\sin^2\theta \cos^2\phi \right) \\ &= -0.4570457994644658 \cdot x \cdot (4z^2 - x^2 - y^2) \end{align}\]\(m=2\)
\[\begin{align} Y_{l=3}^{m=2}(\theta, \phi) &= \sqrt{2} \cdot K_{3}^{2} \cdot \cos(2\phi) \cdot P_{3}^{2}(\cos\theta) \\ &= \sqrt{2} \cdot \Ksqrt{3}{2} \cdot \cos(2\phi) \cdot 15 \cos\theta \sin^2\theta \\ &= \frac{1}{4} \sqrt{\frac{105}{\pi}} \cdot (\cos^2\phi \sin^2\theta- \sin^2\phi \sin^2\theta) \cdot \cos\theta \\ &= 1.445305721320277 \cdot (x^2 - y^2) \cdot z \end{align}\]\(m=3\)
\[\begin{align} Y_{l=3}^{m=3}(\theta, \phi) &= \sqrt{2} \cdot K_{3}^{3} \cdot \cos(3\phi) \cdot P_{3}^{3}(\cos\theta) \\ &= \sqrt{2} \cdot \Ksqrt{3}{3} \cdot \cos(3\phi) \cdot (-15) \sin^3\theta \\ &= -\frac{1}{4} \sqrt{\frac{35}{2\pi}} \cdot \cos(3\phi) \cdot \sin^3\theta \\ &= -\frac{1}{4} \sqrt{\frac{35}{2\pi}} \cdot (4 \cos^3\phi - 3 \cos\phi) \cdot \sin^3\theta \\ &= -\frac{1}{4} \sqrt{\frac{35}{2\pi}} \cdot (\sin\theta \cos\phi) (4 \cos^2\phi \sin^2\theta - 3 \sin^2\theta) \\ &= -\frac{1}{4} \sqrt{\frac{35}{2\pi}} \cdot (\sin\theta \cos\phi) [ \sin^2\theta (\cos^2\phi+ 3 \cos^2\phi - 3 )] \\ &= -\frac{1}{4} \sqrt{\frac{35}{2\pi}} \cdot (\sin\theta \cos\phi) [ \sin^2\theta (\cos^2\phi- 3 \sin^2\phi)] \\ &= -\frac{1}{4} \sqrt{\frac{35}{2\pi}} \cdot (\sin\theta \cos\phi) (\sin^2\theta \cos^2\phi- 3\sin^2\theta \sin^2\phi) \\ &= -0.5900435899266435 \cdot x \cdot [x^2 - 3y^2] \end{align}\]In the code the coefficients are defined as:
C3 = [
-0.5900435899266435,
2.890611442640554,
-0.4570457994644658,
0.3731763325901154,
-0.4570457994644658,
1.445305721320277,
-0.5900435899266435
]
# (Other intermediate lines of code are omitted for brevity)
xx, yy, zz = x * x, y * y, z * z
xy, yz, xz = x * y, y * z, x * z
result = (result +
C3[0] * y * (3 * xx - yy) * sh[..., 9] +
C3[1] * xy * z * sh[..., 10] +
C3[2] * y * (4 * zz - xx - yy)* sh[..., 11] +
C3[3] * z * (2 * zz - 3 * xx - 3 * yy) * sh[..., 12] +
C3[4] * x * (4 * zz - xx - yy) * sh[..., 13] +
C3[5] * z * (xx - yy) * sh[..., 14] +
C3[6] * x * (xx - 3 * yy) * sh[..., 15])
